Details werden zu gegebener Zeit hier sowie in PAUL bekannt gegeben.

Voraussetzungen

Analysis 2
Lineare Algebra

Ziel der Veranstaltung

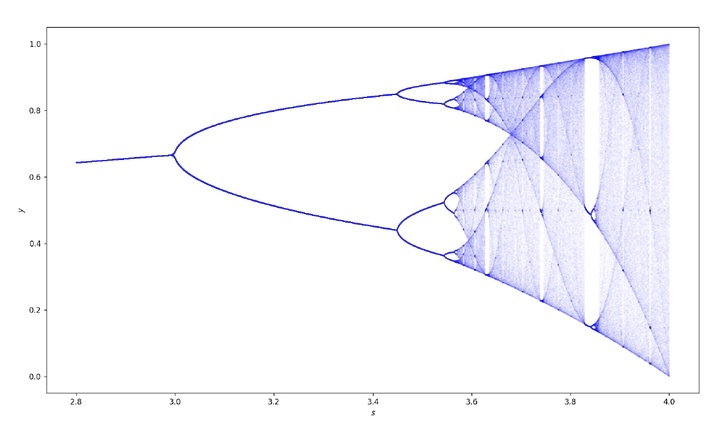
In dieser Vorlesung lernen Sie das faszinierende dynamische Verhalten von diskreten dynamischen Systemen kennen. Mit sehr einfachen Mitteln (eindimensionale, polynomielle Systeme) lassen sich hochkomplexe Phänomene wie deterministisches Chaos erzeugen. In dieser Veranstaltung widmen wir uns diesen Systemen systematisch entwickeln Methoden zur Analyse ihres Verhaltens.

Zielgruppe

B. Sc. (Techno-)Mathematik
M. Sc. Lehramt Mathematik

Inhalte

Diskrete dynamische Systeme sind ein wichtiges Werkzeug zur einfachen, zeitdiskreten Modellierung von zeitveränderlichen Prozessen. Sie entstehen aber auch bei der Diskretisierung (zum Beispiel zur numerischen Behandlung) von zeitkontinuierlichen Systemen. Sie haben daher große Relevanz für eine Vielzahl von Anwendungen wie Klimawissenschaften, Verkehrsmodellierung, Populationsdynamik…

Diskrete dynamische Systeme werden oftmals durch die Iteration, also das wiederholte Ausführen, einer Funktion erzeugt. Trotzdem können schon sehr einfache Funktionen zu hochgradig komplexem Verhalten führen.

In dieser Veranstaltung werden wir diskrete dynamische Systeme systematisch einführen, ihre wesentlichen Eigenschaften beschreiben und intuitive sowie analytische Methoden zu Ihrer Analyse entwickeln. Der Hauptfokus liegt auf eindimensionalen Systemen. Im letzten Teil gehen wir dann auch auf höherdimensionale Systeme ein.

Die wesentlichen Themengebiete sind

• Orbits, Fixpunkte, periodische Punkte, …
• (Asymptotische) Stabilität
• Bifurkationen
• Chaotische Dynamik
• Fraktale und nicht ganzzahlige Dimension
• Lineare und nichtlineare Systeme

Informationen zur Leistungserbringung

Erfolgreiche Teilnahme an den Übungen und der Klausur

Literatur

Erster Teil:

• R. L. Devaney
  An Introduction To Chaotic Dynamical Systems (3rd ed.)
  Chapman and Hall/CRC, 2021.
  Erste Edition in der Universitätsbibliothek verfügbar.

Zweiter Teil:

• U. Krause, T. Nesemann
  Differenzengleichungen und diskrete dynamische Systeme
  De Gruyter, Berlin, 2012.
  Volltext über die Universitätsbibliothek zum Download verfügbar.

Weitere Quellen werden bei Bedarf im Verlauf der Vorlesung bekannt gegeben.

Ergänzende Veranstaltungen

Die Vorlesung eignet sich gut als Aufbauveranstaltung zum Seminar „Computational Dynamics“, das im Wintersemester 2025/26 angeboten wurde. Einige Seminarthemen werden hier vertieft behandelt. Die vorherige Teilnahme am Seminar ist allerdings auch für das Verständnis der Vorlesungsinhalte keinesfalls erforderlich.

Termine

• Montag 8:00 - 11:00 Uhr, Raum D 1 320
• Dienstag 9:00 - 11:00 Uhr, Raum D 1 320