Poster: Systematic construction of hierarchical connection structures in phase space

Abstract

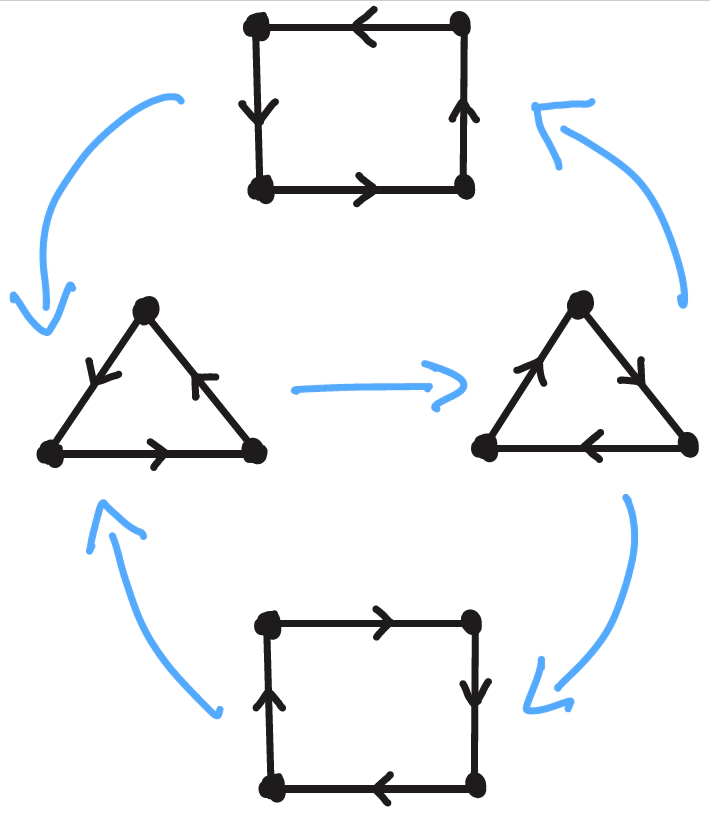
We provide a method to systematically construct vector fields that possess excitable transitions corresponding to a desired hierarchical connection structure. The structure is given as a finite set of digraphs $G_1,…,G_N$ (the lower level), together with another digraph $\Gamma$ on the set of nodes $1,…,N$ (the top level). The dynamic realizations of $G_1,…,G_N$ are heteroclinic networks and they can be thought of as individual connection patterns on a given set of states. Connections in $\Gamma$ correspond to transitions between these different connection patterns. In our construction, the connections given through $\Gamma$ are not heteroclinic, but excitable with zero threshold: such a connection exists between two sets $S,S’$ if in every $\delta$-neighbourhood of $S$ there is at least one initial condition such that its $\omega$-limit is contained in $S’$. In this sense, we prove a theorem that allows the systematic creation of hierarchical networks that are excitable on the top level, and heteroclinic on the lower level. Our results modify and extend the simplex method by Ashwin & Postlethwaite, which is one of several existing techniques for the construction of vector fields that possess a desired heteroclinic network.

I am presenting this poster jointly with Alexander Lohse (Universität Hamburg)

Sören von der Gracht

Mathematician researching dynamical systems

Research in network dynamical systems and its applications.